链表是否存在环？

描述

141. Linked List Cycle

Given a linked list, determine if it has a cycle in it.

思路

使用两个指针，一个每次走两步，一个每次走一步，如果一段时间之后这两个指针能重合，那么链表就存在环了。 但是，这不是一个充要条件，两个指针相遇，我们可以通过反证法轻易证明链表存在环；链表存在环，两个指针就一定会相遇吗？

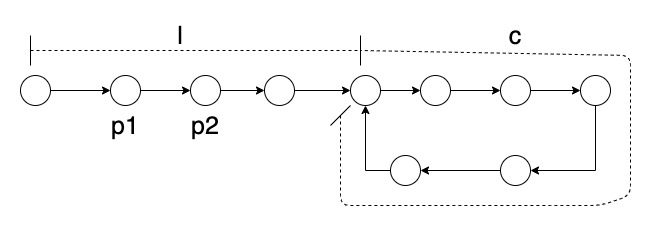
现在就来证明一下吧。

如图，我们记环开始前的距离为 l，环长为 c, p1 前进的距离为 f1(t)，p2 前进的距离为 f2(t)，t 表示时间。 要证明两个指针相遇，等价于证明：

存在正整数 t 和 n，使得 f2(t) - f1(t) = n * c，且 f2(t) - f1(t) >= l，其中 f2(t) = 2 * t f1(t) = t

当 c >= l 时，取 t = c， n = 1 即可满足上述命题；

当 c < l 时，取 t = ceil(l / c) * c， n = ceil(l / c)，其中 ceil表示向上取整， 即可满足上命题

解答

# Definition for singly-linked list.
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if not head or not head.next:
            return False
        p1, p2 = head, head.next
        while not (p1 is p2) and (p2 and p2.next and p2.next.next):
            p1 = p1.next
            p2 = p2.next.next
        if p1 is p2:
            return True
        return False

标签： Easy、 链表